算法图解7 - 动态规划
动态规划作为算法的必考内容,重要性不言自明。如何理解动态规划,并能够应用到实际场景中,这是本节的重点。
一、动态规划
动态规划功能强大,它能够解决子问题并使用这些答案来解决大问题。
但仅当每个子问题都是离散的,即不依赖于其他子问题时,动态规划才管用。
二、解决方案
1.每种动态规划解决方案都涉及网格。
2.单元格中的值通常就是你要优化的值。在前面的背包问题中,单元格的值为商品的价值。
3.每个单元格都是一个子问题,因此你应考虑如何将问题分成子问题,这有助于你找出网格的坐标轴。
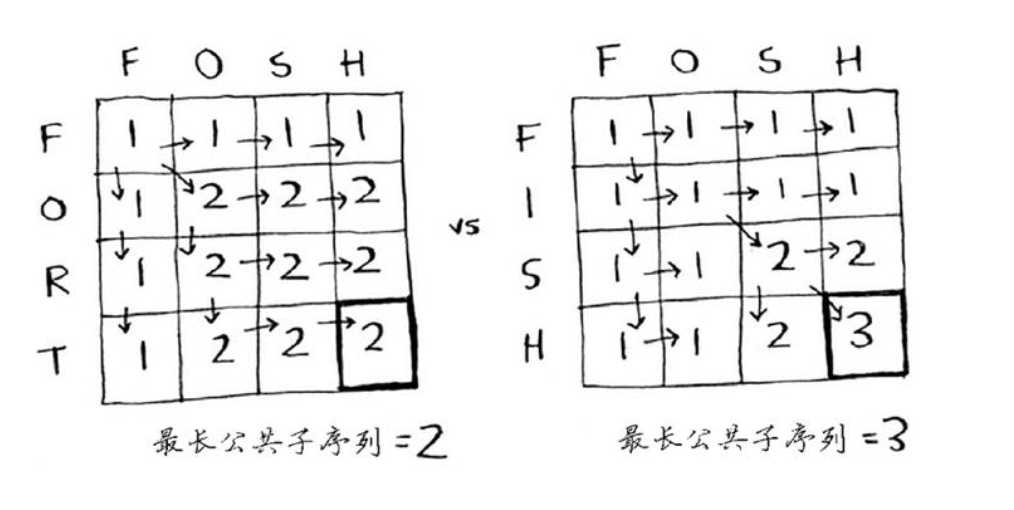
三、最长公共子序列之解决方案
我们来看看网格法求 FORT 和 FOSH,首先绘制如下网格:
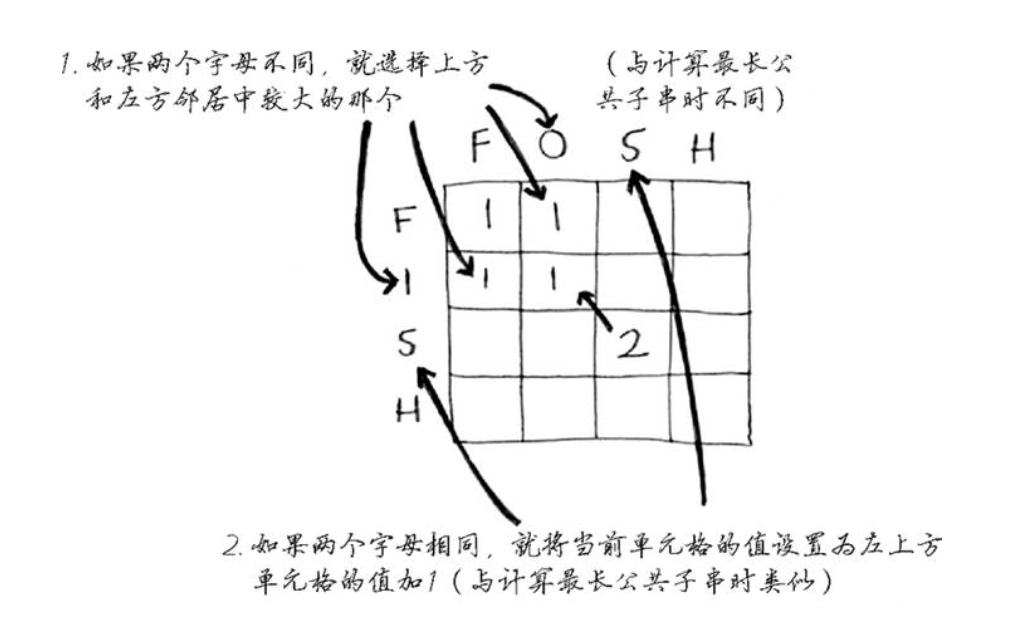
具体的思路如下:
按照上面的分析,核心代码片段可能如下:1
2
3
4if word_a[i] == word_b[j]: ←--------两个字母相同
cell[i][j] = cell[i-1][j-1] + 1
else: ←------------------------------两个字母不同
cell[i][j] = max(cell[i-1][j], cell[i][j-1])
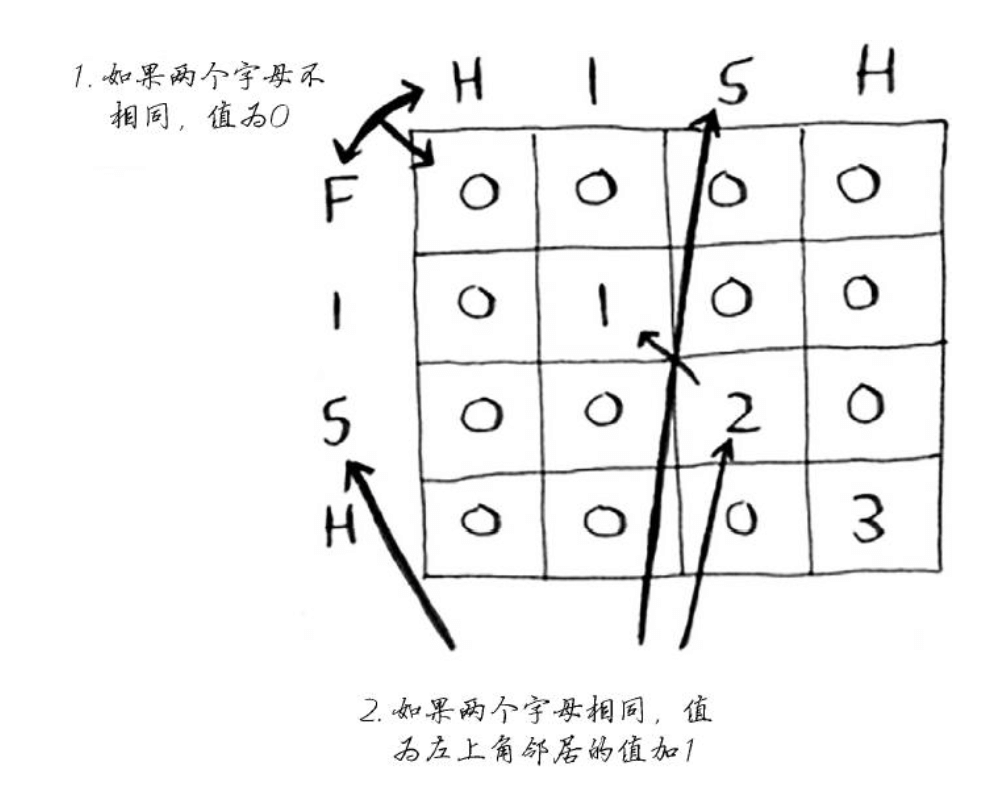
四、最长公共子串
如上图,核心代码片段可能如下:1
2
3
4if word_a[i] == word_b[j]: ←---------两个字母相同
cell[i][j] = cell[i-1][j-1] + 1
else: ←------------------------------两个字母不同
cell[i][j] = 0
五、实际应用
编写一个函数来查找字符串数组中的最长公共前缀。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16/**
* @param {string[]} strs
* @return {string}
*/
var longestCommonPrefix = function(strs) {
if(strs.length === 0) return '';
let result = '';
let len = Math.min.apply(Math, strs.map(item => item.length));
for(let i = 0; i < len; i++) {
let tmp = strs.map(item => item.substring(0, i+1));
if (new Set(tmp).size === 1) result = tmp[0];
}
return result;
};
// 输入: ["flower","flow","flight"]
// 输出: "fl"