算法图解1 - 二分查找和大O表示法
闲来无事,翻了翻《算法图解》,觉得收获颇多,所以会陆续整理成笔记,纪录学习过程。嗯,第一篇先来看看二分查找和大O表示法吧。
一、二分查找
二分查找是一种算法,其输入是一个有序的元素列表(必须有序的原因稍后解释)。如果要查找的元素包含在列表中,二分查找返回其位置;否则返回 null 。
一般而言,对于包含 n 个元素的列表,用二分查找最多需要 log2 n 步,而简单查找最多需要 n 步。
很多童鞋可能忘了倒数如何计算,这里我们先复习一下:对数运算是幂运算的逆运算。看看下面的公式,是不是有点回忆起来了。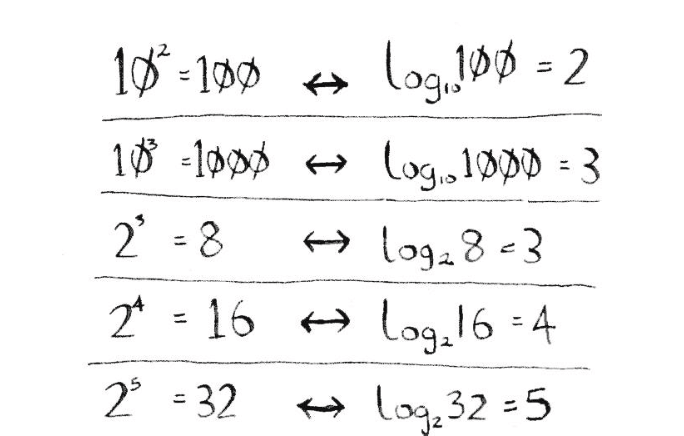
我们通过 JS 来实现一下思路:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25/**
* @msg: 二分查找
* @param {Array} 数组
* @param {String} 数值
* @return: index
*/
const binarySearch = (arr, val) => {
let start = 0;
let end = arr.length - 1;
let guess;
while (start <= end) {
let mid = Math.ceil((start + end) / 2);
guess = arr[mid];
if (guess === val) return mid;
if (guess > val) {
end = mid - 1;
} else {
start = mid + 1;
}
}
return -1;
}
binarySearch([1, 3, 5, 7, 9], 3);
一般而言,应选择效率最高的算法,以最大限度地减少运行时间或占用空间。
按照上面的思路,我们使用二分查找实现了这个函数。嗯,看起来不错,我们来看看他的运行时间。
二、运行时间
先来看一个概念:
线性时间(linear time):最多需要猜测的次数与列表长度相同,这被称为线性时间。
我们举个例子来说:简单查找逐个地检查数字,如果列表包含 100 个数字,最多需要猜 100 次。如果列表包含 40 亿个数字,最多需要猜 40 亿次。
二分查找则不同:如果列表包含 100 个元素,最多要猜 7 次;如果列表包含 40 亿个数字,最多需猜 32 次。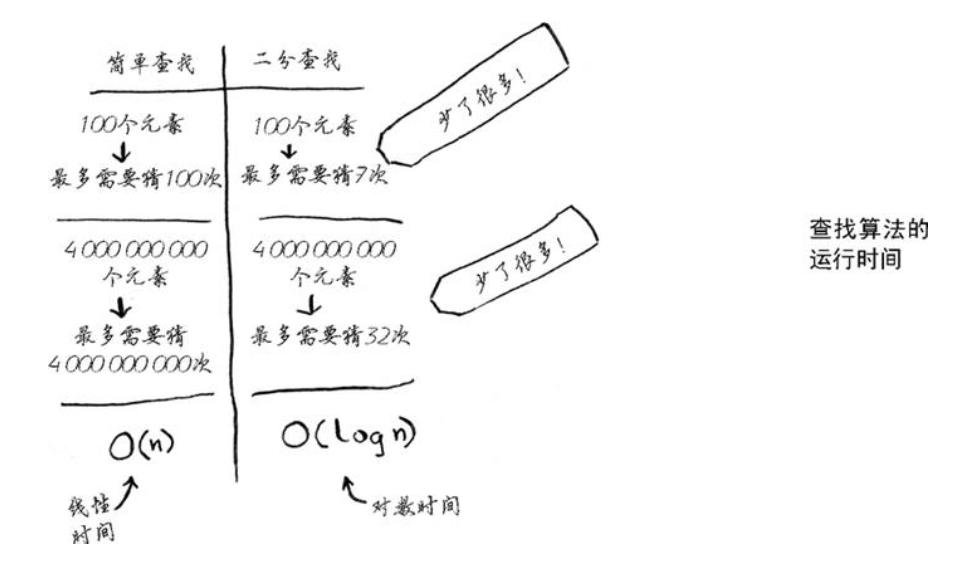
可以看出来,对比线性查找来说,二分查找效率出奇的高。
既然提到运行时间,那么我们一般如何来计量呢?
三、大O表示法
大O表示法:是一种特殊的表示法,指出了算法的速度有多快。。
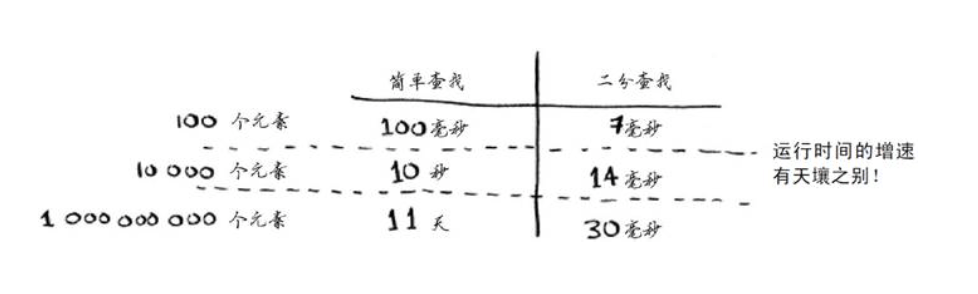
通过上图,我们不难看出来:
随着元素数量的增加,二分查找需要的额外时间并不多,而简单查找需要的额外时间却很多。因此,随着列表的增长,二分查找的速度比简单查找快得多。
有鉴于此,仅知道算法需要多长时间才能运行完毕还不够,还需知道运行时间如何随列表增长而增加。这正是大O表示法的用武之地。使用大O表示法,这个运行时间为 O (n )。单位秒呢?没有——大O表示法指的并非以秒为单位的速度。
大O表示法让你能够比较操作数,它指出了算法运行时间的增速。
需要注意:大O表示法计算的是操作数。
这里有个问题:
如果要查找的是 Adit ——电话簿中的第一个人,一次就能找到,无需查看每个条目。考虑到一次就找到了 Adit,请问这种算法的运行时间是 O(n) 还是 O(1) 呢?
大O表示法说的是最糟的情形。
因此,你可以说,在最糟情况下,必须查看电话簿中的每个条目,对应的运行时间为 O(n)。这是一个保证——你知道简单查找的运行时间不可能超过 O(n)。
四、5种常见大O运行时间
- 对数时间:O (log n ),二分查找
- 线性时间:O (n ) ,简单查找
- O (n * log n ),快速排序——一种速度较快的排序算法
- O (n 2 ),选择排序——一种速度较慢的排序算法
- O (n !),旅行商问题的解决方案——一种非常慢的算法
我们来举个例子,绘制一个包含 16 格的网格,且有 5 种不同的算法可供选择,下面按从快到慢的顺序列出了使用这些算法绘制网格所需的时间:
这就有意思了,通过上面的图示,我们得到几点启示
1.算法的速度指的并非时间,而是操作数的增速。
2.谈论算法的速度时,我们说的是随着输入的增加,其运行时间将以什么样的速度增加。
3.算法的运行时间用大O表示法表示。
4.O (log n ) 比 O (n ) 快,当需要搜索的元素越多时,前者比后者快得越多。
五、旅行商问题
上面提到了一种运行时间为 O (n !) 的算法,提到了旅行商问题,这里我们来扩展一下。
这着实困扰着很多人,一位旅行商要去往 5 个城市,如何确保旅程最短,5 个城市有 120 种不同的排列方式。涉及 n 个城市时,需要执行 n!( n 的阶乘)次操作才能计算出结果。因此运行时间为 O(n!),即阶乘时间。
5 个城市,有 5 种选择,去到一个城市之后,还有 4 种选择,以此类推:5*4*3*2*1 = 5! = 120
旅行商问题(TravelingSalesmanProblem,TSP )是一个经典的组合优化问题。经典的 TSP 可以描述为:一个商品推销员要去若干个城市推销商品,该推销员从一个城市出发,需要经过所有城市后,回到出发地。应如何选择行进路线,以使总的行程最短。
从图论的角度来看,该问题实质是在一个带权完全无向图中,找一个权值最小的 Hamilton 回路。
由于该问题的可行解是所有顶点的全排列,随着顶点数的增加,会产生组合爆炸,它是一个 NP 完全问题。
由于其在交通运输、电路板线路设计以及物流配送等领域内有着广泛的应用,国内外学者对其进行了大量的研究。早期的研究者使用精确算法求解该问题,常用的方法包括:分枝定界法、线性规划法、动态规划法等。
但是,随着问题规模的增大,精确算法将变得无能为力,因此,在后来的研究中,国内外学者重点使用近似算法或启发式算法,主要有遗传算法、模拟退火法、蚁群算法、禁忌搜索算法、贪婪算法和神经网络等。
突然发现,算法的世界真的很大,而很多实际问题都是通过算法解决的。
所以,花些时间了解一下经典算法,也算是提高自己的核心竞争力。
六、文末彩蛋:原来小蜜蜂一直在解决旅行商问题!
进行研究的奈杰尔·雷恩博士说,蜜蜂每天都要在蜂巢和花朵间飞来飞去,为了采蜜而在不同花朵间飞行是一件很耗精力的事情,因此实际上蜜蜂每天都在解决「旅行商问题」。尽管蜜蜂的大脑只有草籽那么大,也没有电脑的帮助,但它已经进化出了一套很好的解决方案,如果能理解蜜蜂怎样做到这一点,对人类的生产、生活将有很大帮助。

