算法图解2 - 数组和链表
我们继续上文的脚步,深入了解一下数组和链表。掌握它们之间的区别和联系,以及各自的使用场景,为后续的算法学习打好基础。
一、计算机内存的工作原理
为了更好的理解数组和链表,我们先来简单介绍一下计算机内存的工作原理。
简单来说:计算机就像是很多抽屉的集合体,每个抽屉都有地址。
需要将数据存储到内存时,你请求计算机提供存储空间,计算机给你一个存储地址。需要存储多项数据时,有两种基本方式:数组和链表。
二、数组
我们先不看概念,来个小例子简单认识一下。
假设我们要编写一个管理待办事项的应用程序,为此需要将这些待办事项存储在内存中。我们先将待办事项存储在数组中。使用数组意味着所有待办事项在内存中都是相连的(紧靠在一起的)。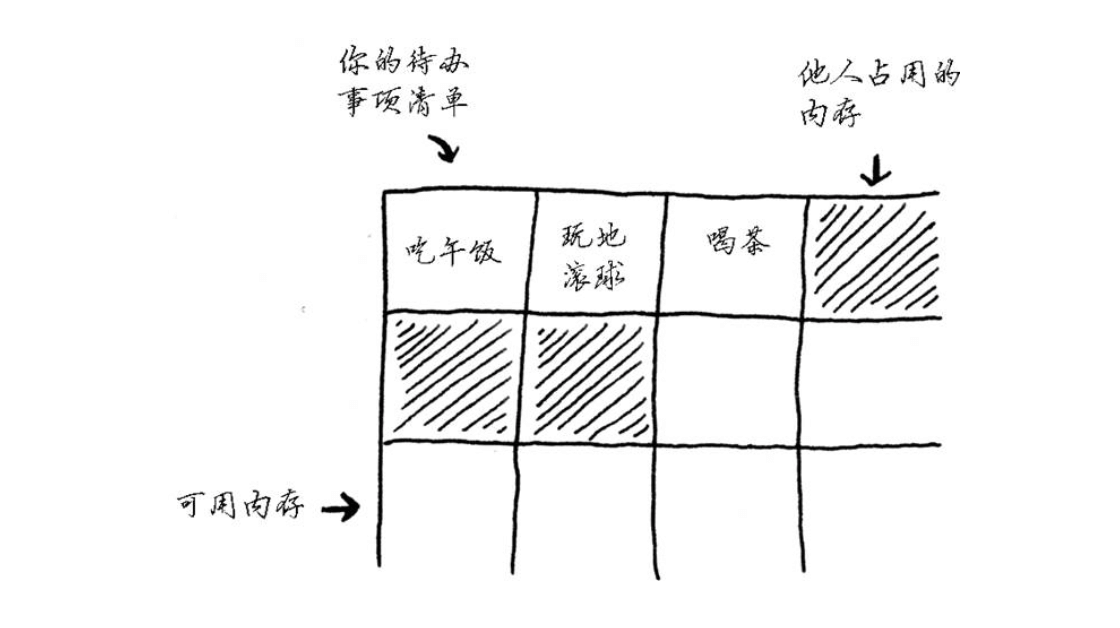
现在假设你要添加第四个待办事项,但后面的那个抽屉放着别人的东西!在这种情况下,你需要请求计算机重新分配一块可容纳 4 个待办事项的内存,再将所有待办事项都移到那里。
那么问题来了,如果我又有了第 5 个待办事项,这时候,又得进行一次大转移。
那么有没有什么解决方案呢?答案是肯定的,但是并不完美。譬如,我们直接申请 10 个内存单元,这样就可以继续6,7,8,9,10。
这是一个不错的权变措施,但是它存在如下两个缺点:
1.你额外请求的位置可能根本用不上,这将浪费内存。你没有使用,别人也用不了。
2.待办事项超过 10 个后,你还得转移。
看起来我们的方案并不完美,那么有什么好的办法吗?
三、链表
链表中的元素可存储在内存的任何地方。
我们继续用上面的例子: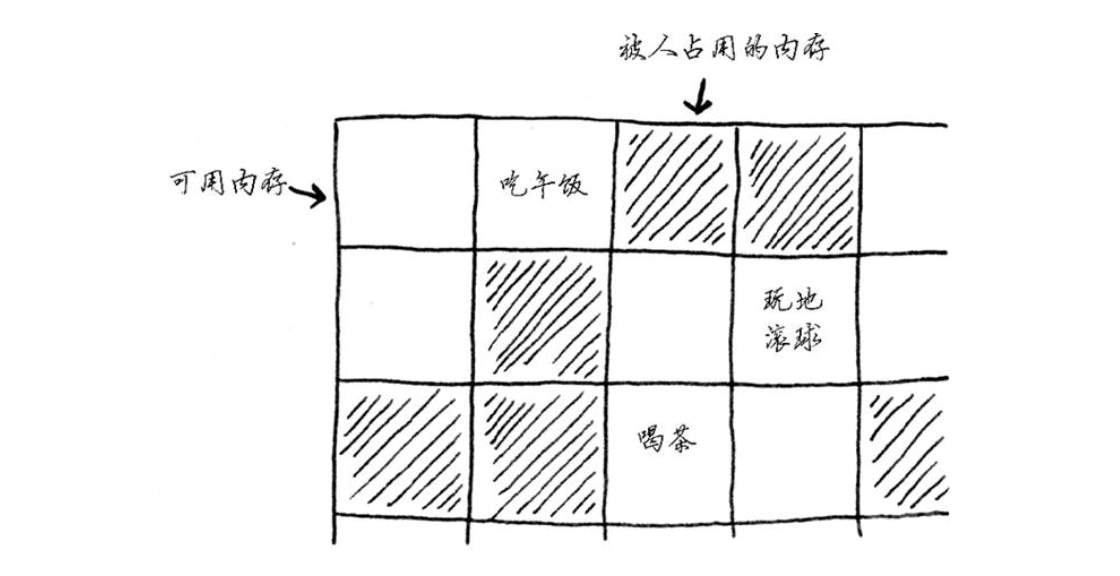
链表的每个元素都存储了下一个元素的地址,从而使一系列随机的内存地址串在一起。
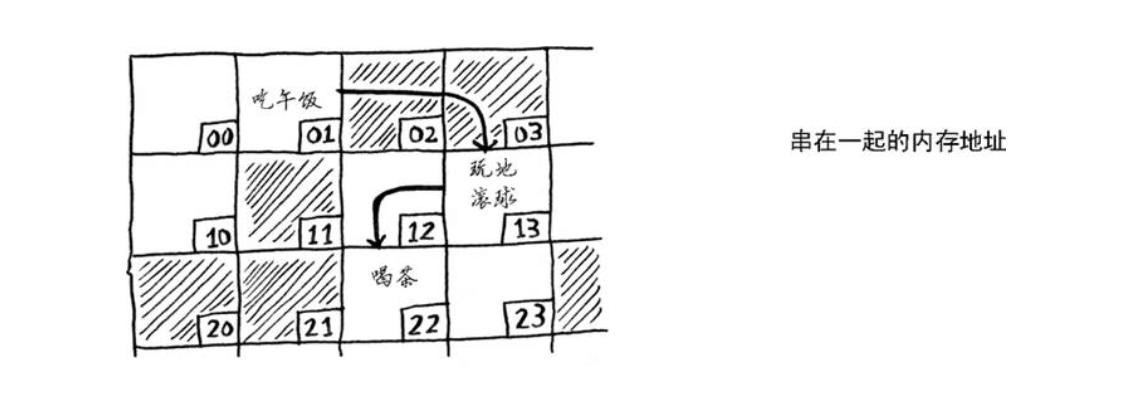
这犹如寻宝游戏。你前往第一个地址,那里有一张纸条写着“下一个元素的地址为123”。因此,你前往地址123,那里又有一张纸条,写着“下一个元素的地址为847”,以此类推。在链表中添加元素很容易:只需将其放入内存,并将其地址存储到前一个元素中。
只要有足够的内存空间,就能为链表分配内存。
链表的优势在插入元素方面,那数组的优势又是什么呢?
四、优缺点对比
1.先来看看链表
在链表中,元素并非靠在一起的,你无法迅速计算出第五个元素的内存地址,而必须先访问第一个元素以获取第二个元素的地址,再访问第二个元素以获取第三个元素的地址,以此类推,直到访问第五个元素。
链表有两个特点:
- 需要同时读取所有元素时,链表的效率很高:你读取第一个元素,根据其中的地址再读取第二个元素,以此类推。
- 如果你需要跳跃,链表的效率真的很低。
2.数组与此不同
在数组中我们知道其中每个元素的地址。例如,假设有一个数组,它包含五个元素,起始地址为 00,那么元素 #5 的地址 04,这个很容易就能知道。
需要随机地读取元素时,数组的效率很高,因为可迅速找到数组的任何元素。
所以我们可以总结出一些规律:
- 数组读取运行时间 O ( 1 ),插入运行时间 O ( n );
- 链表读取运行时间 O ( n ),插入运行时间 O ( 1 );
五、适用场景
有两种访问方式:随机访问和顺序访问 。
顺序访问意味着从第一个元素开始逐个地读取元素。链表只能顺序访问:要读取链表的第十个元素,得先读取前九个元素,并沿链接找到第十个元素。随机访问意味着可直接跳到第十个元素。
我们经常说数组的读取速度更快,这是因为它们支持随机访问。当然,数组和链表还被用来实现其他数据结构,后面我们细说。
链表擅长插入和删除,而数组擅长随机访问。
六、选择排序
有了上面的基础,我们来学习一下:选择排序。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26/**
* @msg: 选择排序
* @param {Array} arr
* @return: Array
*/
const selectionSort = (arr) => {
let newArr = [];
let len = arr.length;
for (let i = 0; i < len; i++) {
let smallest = arr[0];
let smallest_index = 0;
for(let j = 1; j < len - 1; j++) {
if (arr[j] < smallest) {
smallest = arr[j];
smallest_index = j;
}
}
newArr.push(arr.splice(smallest_index,1)[0]);
}
return newArr;
}
selectionSort([5, 3, 6, 2, 10]);
书中用 Python 实现,这里我们采用了 JS 实现,先实现为主,后续进行算法优化。

