算法图解5 - 图和广度优先搜索
一直以来总是把「数据结构」和「算法」分的很开,认为图,链表都应该属于数据结构领域。然后当看到书的后面章节时,才发现有些东西并不需要明显的界限。
一、图是什么?
图模拟一组连接。
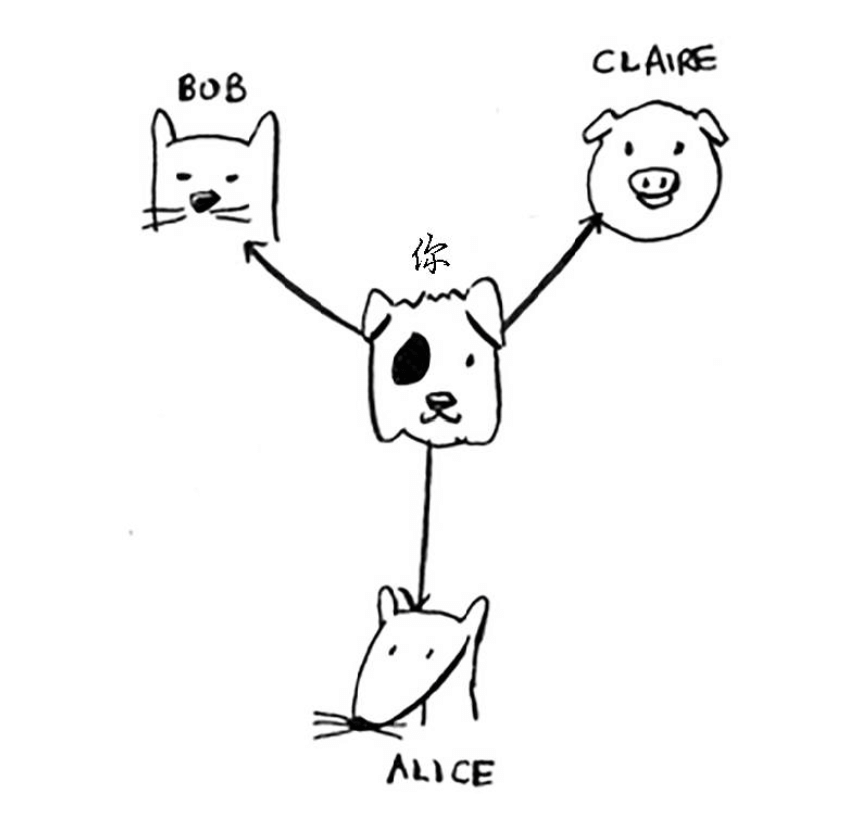
是不是觉得很抽象?别着急,我们打个比方,朋友一起打牌,我们要记录谁欠谁钱:
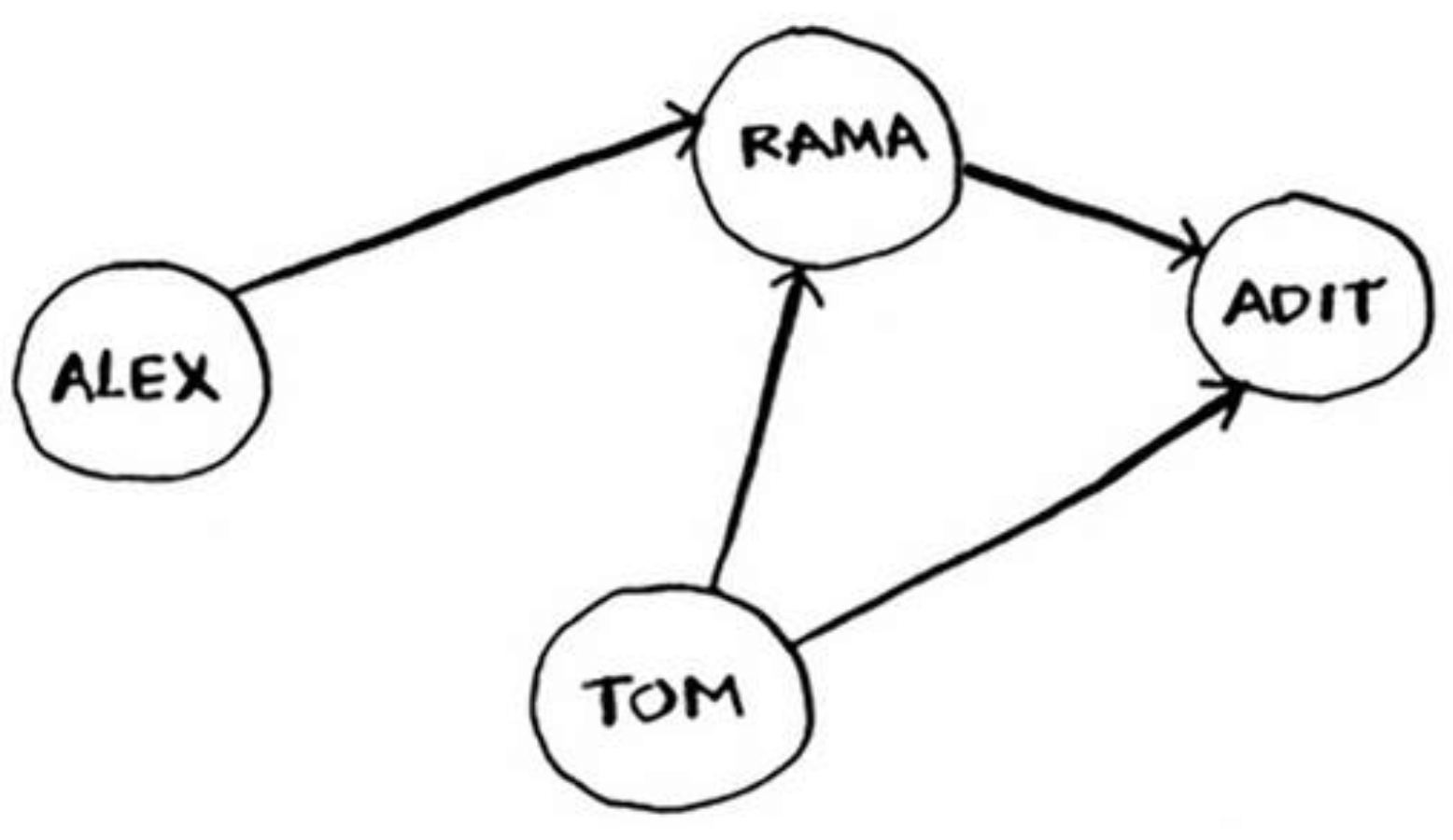
欠钱关系可能如下所示:
好了,是时候引出我们的概念:
1.图由节点 node 和边 edge 组成。
2.一个节点可能与众多节点直接相连,这些节点被称为邻居。
在前面的欠钱图中,Rama 是 Alex 的邻居。Adit 不是 Alex 的邻居,因为他们不直接相连。但 Adit 既是 Rama 的邻居,又是 Tom 的邻居。
3.图用于模拟不同的东西是如何相连的。
二、图的表示
我们可以用散列表来表示图,那么在 JS 中呢,当然就是 Hash Map 了。
1 | let graph = new Map(); |
来看看输出:
关于图,有几点需要注意:
1.图中的每个节点都需要表示;
2.键值对的添加顺序对结果没有影响,因为散列表是无序的;
三、有向图和无向图
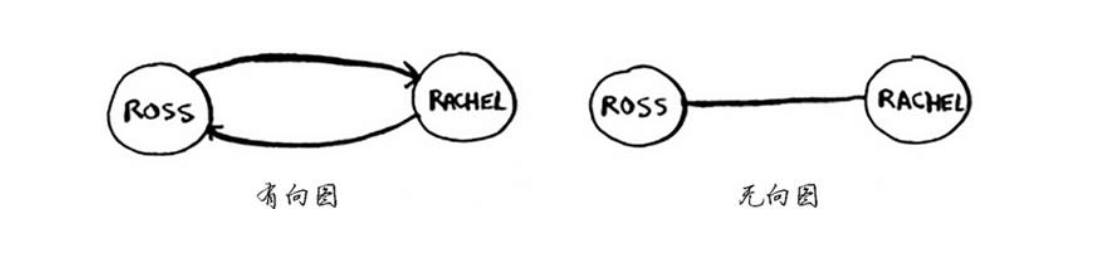
要区别这两个概念,我们先来看下面这张图:
有向图:有指向邻居的箭头,其中的关系是单向的。
无向图:
undirected graph 没有箭头,直接相连的节点互为邻居。
无向图中的边不带箭头,其中的关系是双向的。
四、图的实现
说了这么多,那么如何代码实现呢?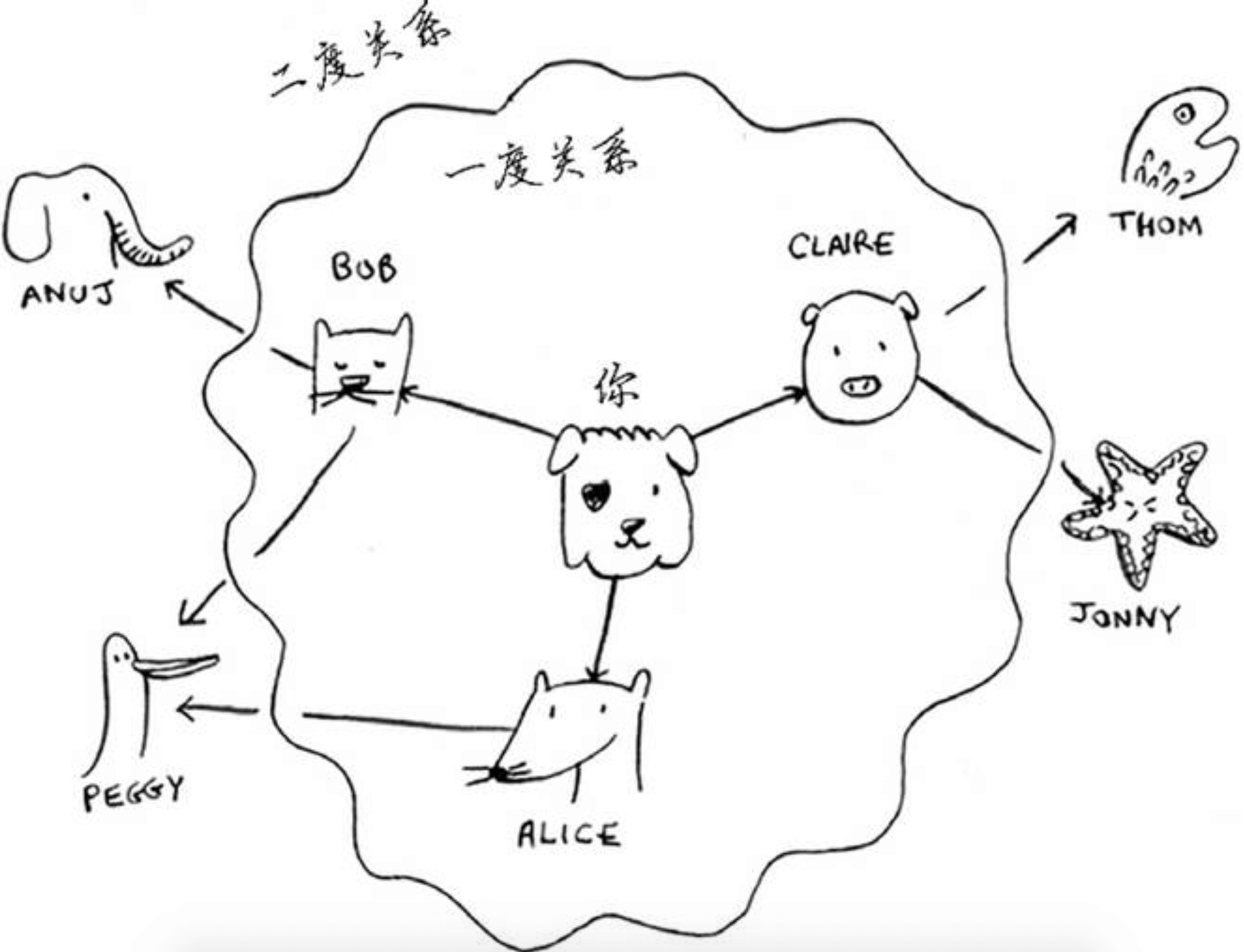
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38// 定义散列表
let graph = new Map();
graph.set('jartto', ['alice', 'bob', 'claire']);
graph.set('bob', ['anuj', 'peggy']);
graph.set('alice', ['peggy']);
graph.set('claire', ['thom', 'jonny']);
graph.set('anuj', []);
graph.set('peggy', []);
graph.set('thom', []);
graph.set('jonny', []);
// 查询函数
function search(name) {
let queue = [];
let searched = [];
queue = queue.concat(graph.get(name));
while (queue.length > 0) {
person = queue.shift();
if (!searched.includes(person)) {
if (isSeller(person)) {
console.log(`${person} is a mango seller`);
return true;
} else {
queue = queue.concat(graph.get(person));
searched.push(person);
}
}
}
return false;
}
// 检查人的姓名是否以m结尾:如果是,他就是芒果销售商。
function isSeller(name) {
return name[name.length-1] == 'm';
}
search('jartto');
五、广度优先搜索
广度优先搜索是一种用于图的查找算法,可帮助回答两类问题。
1.从节点 A 出发,有前往节点 B 的路径吗?
2.从节点 A 出发,前往节点 B 的哪条路径最短?
解决最短路径问题的算法被称为广度优先搜索 。
我们来打个比方,朋友是一度关系,朋友的朋友是二度关系。像下面这张图: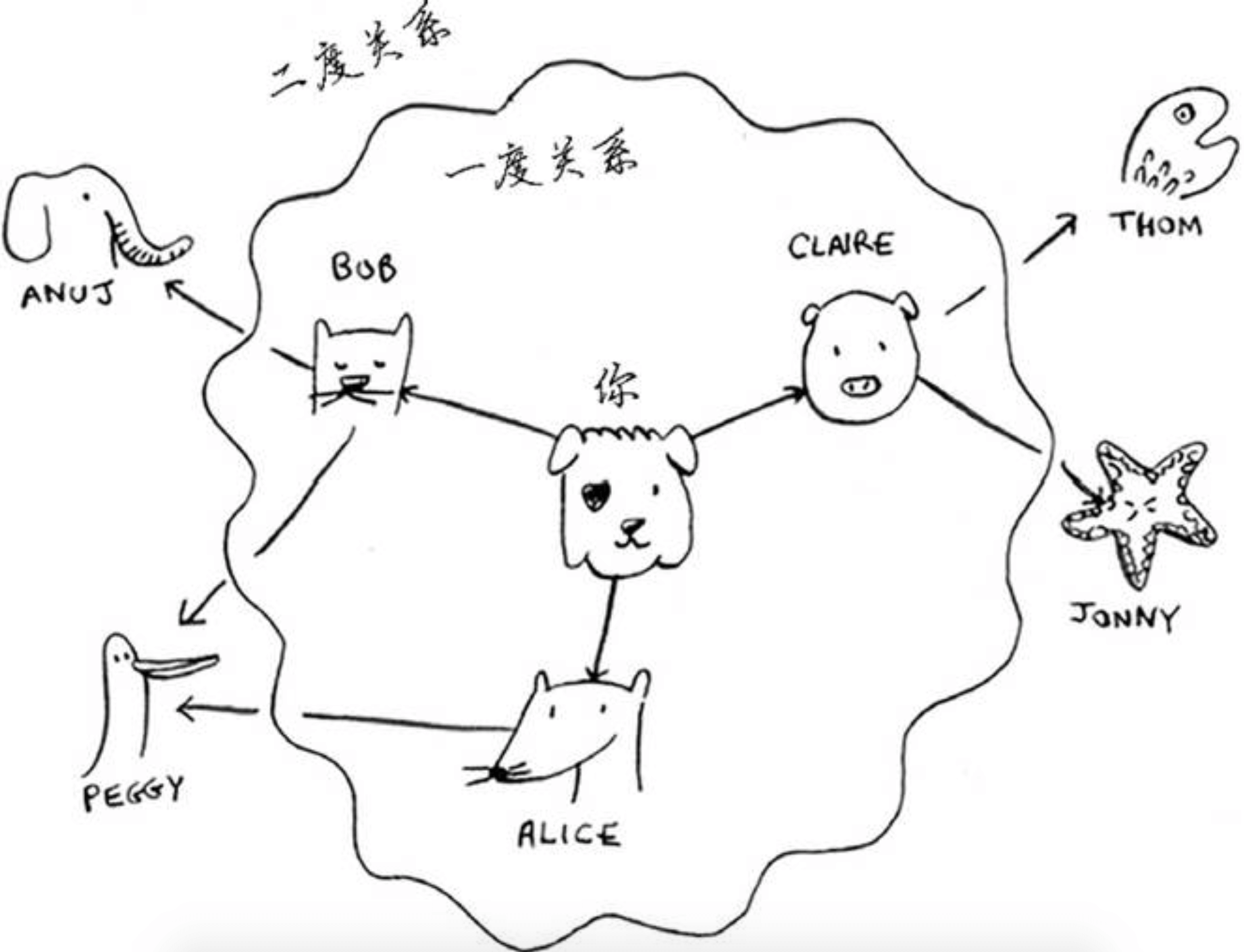
在广度优先搜索的执行过程中,搜索范围从起点开始逐渐向外延伸,即先检查一度关系,再检查二度关系。
广度优先搜索不仅查找从A到B的路径,而且找到的是最短的路径。
六、广度优先搜索使用场景
1.编写国际跳棋 AI,计算最少走多少步就可获胜;
2.编写拼写检查器,计算最少编辑多少个地方就可将错拼的单词改成正确的单词,如将 READED 改为 READER 需要编辑一个地方;
3.根据你的人际关系网络找到关系最近的医生。
七、运行时间
如果你在你的整个人际关系网中搜索芒果销售商,就意味着你将沿每条边前行(记住,边是从一个人到另一个人的箭头或连接),因此运行时间至少为 O (边数)。
你还使用了一个队列,其中包含要检查的每个人。将一个人添加到队列需要的时间是固定的,即为 O(1),因此对每个人都这样做需要的总时间为 O (人数)。
所以,广度优先搜索的运行时间为 O (人数 + 边数),这通常写作 O(V + E ),其中 V 为顶点 vertice 数,E 为边数。
八、扩展:拓扑排序
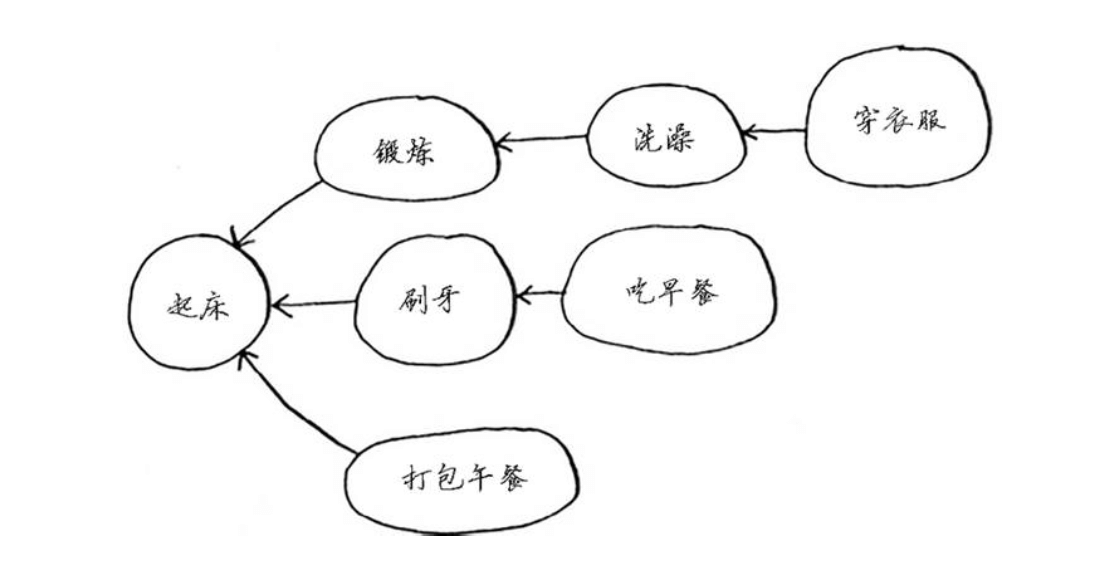
从某种程度上说,这种列表是有序的。如果任务 A 依赖于任务 B ,在列表中任务 A 就必须在任务 B 后面。这被称为拓扑排序 ,使用它可根据图创建一个有序列表。